题目大意
给定n个基本词汇和m个禁忌词汇,求用这n个串组成长度l的串的方案数
数据范围
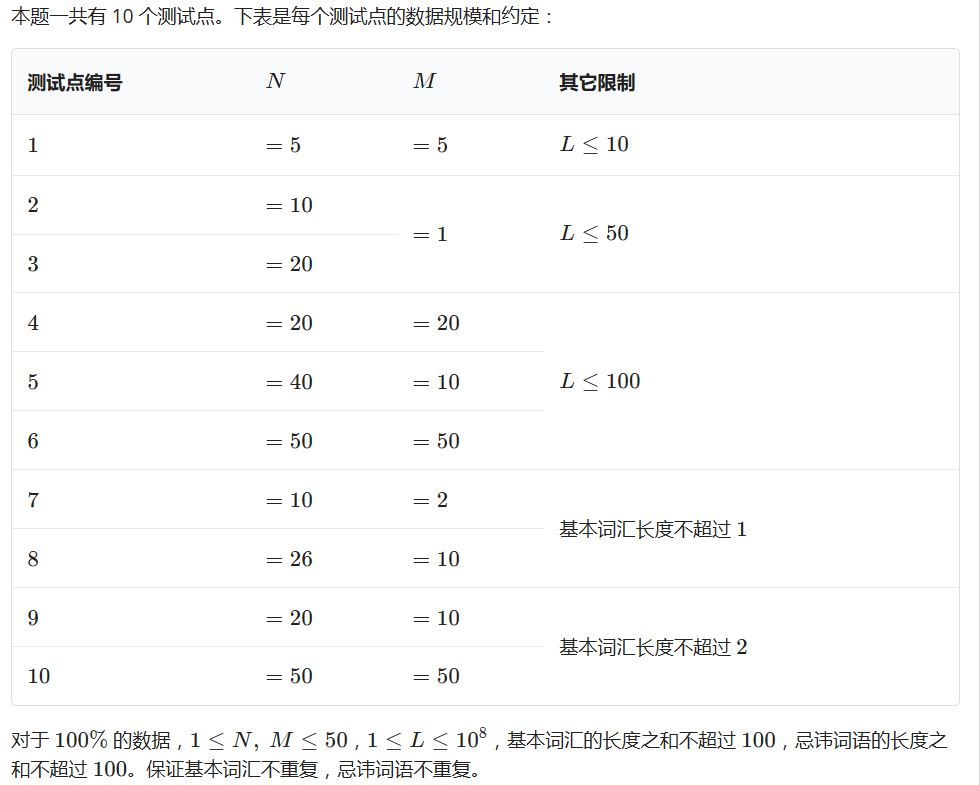
算法讨论
AC自动机DP
$状态:f[i][j]表示已经组成了长度为i的串,停留在自动机上第j个点的方案数$
$转移:f[i + len[k]][run(j,len[k])] += f[i][j]$
这样可以过前6组数据,注意AC自动机上每个点的$flag$会影响$fail$子树的$flag$
对于后面四组数据,DP就不行了,可以考虑矩阵乘法
对于词汇长度为1的,直接按照自动机的转移建矩阵,对于长度为2的,就扩大矩阵,记录一下前一次的状态就好了
1 |
|